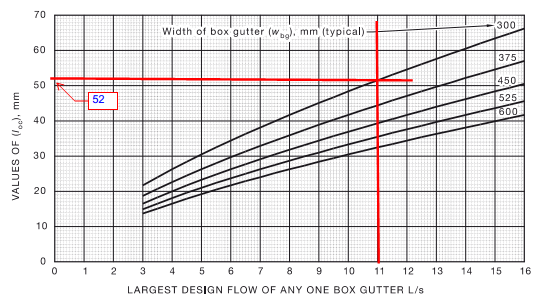
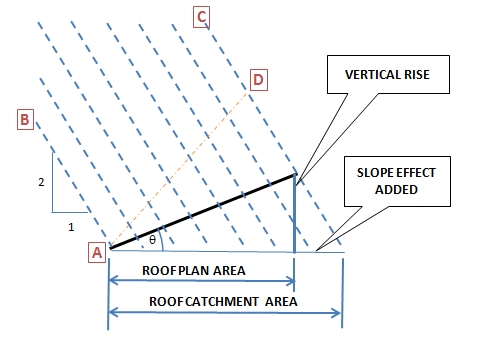
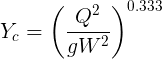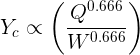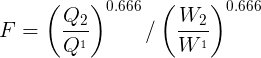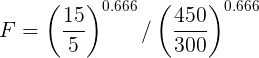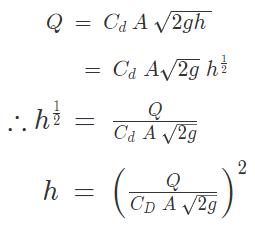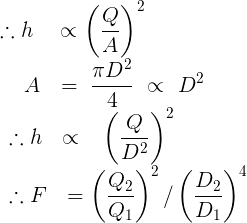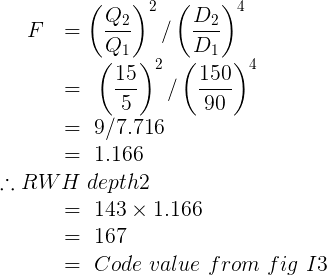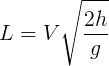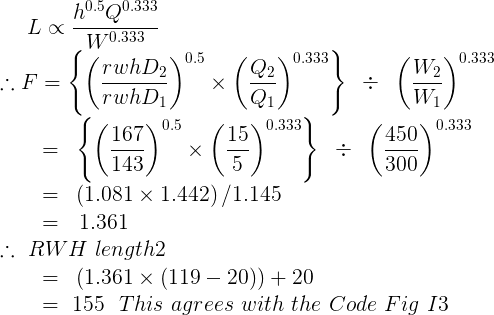Author: KenS

Hi there, welcome to my blog.
I am a retired Charted Professional Engineer (CPEng), with an embarrassing amount of experience, which I would like to pass on before I forget everything.
For more details check out the "About Me" link at the top of this page or for some great free calculators check out the web site.

July 21, 2023

What does an eaves gutter look like when it just starts to overflow?

When a downpipe gets blocked we have to design for overflow conditions.

‌This normally allows for the water to overflow either the front or the back of the gutter.

We assume the water overflows equally along the full length of the gutter.

We then use the weir formula to calculate the depth of water overflowing. shown as “h” in the above diagrams.

Knowing this depth allows us to adjust the flashing, or the distance below the top of the fascia, to prevent any water from entering the building.

However eaves gutters normally have a slope, so the overflowing edge is not level.

This raises the question, if the downstream end is the lowest, wouldn’t all the water be overflowing there?

Meaning that the code, and all our calculations to date have been wrong?

So, I decided to check it out by using computational fluid Dynamics (CFD).

This is a computer program that plots the motion of every single particle in the water, and gives us a reasonably good idea of what will happen.

Its not the best quality but I had to reduce the file size substantially for it to upload.

So, check it out here…..

February 10, 2019

How to size a box gutter for any flow by using the graphs in the Plumbing Code.

When designing Box Gutters, the graphs in the Plumbing Code only allow for designs between the flows of 3L/s and 16L/s.

With industrial buildings getting much bigger, there is a need to go well outside these limits.

I will now show you how to do this by using the graphs, and associated figures from the Plumbing Code AS/NZS 3500.3 2018

Step one: pick any size box gutter that fits on the relevant graph, and determine the depth, and the rain water head sizes.

Step two: Calculate the necessary scaling factors to scale these dimensions to the flow we want.

However its not quite that easy. Scaling one dimension does not necessarily result in scaling another by the same amount.

For example, scaling the sides of a square by a factor of two, increases the area by a factor of 4.

Fluids are a bit like that. However there are things that can’t be scaled, like gravity, viscosity, surface tension, friction etc.

So how do we find out the resultant scaling factor?

We start by finding an equation relevant to the situation that has all the related variables.

For box gutter depth, any equation incorporating flow, depth and width will do.

The best and simplest is the critical depth equation.

Critical depth occurs near the outfall of every box gutter.

The usual nomenclature applies Q = flow, W = width, Y = depth. Suffix 1 represents the base condition to be scaled, and suffix 2 the scaled result.

Critical depth formula

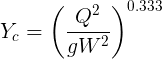
Constants have a scale factor of 1, therefore they are not required, so we can eliminate “g”.

We then say that Yc is proportional to:-

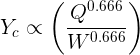
We now find the scale ratio between Q1 & Q2 and W1 & W2 and the resulting multiplying factor F:-

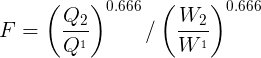
By the way, the slope also can’t be scaled, so the slope must be the same for both gutters.

Try an example

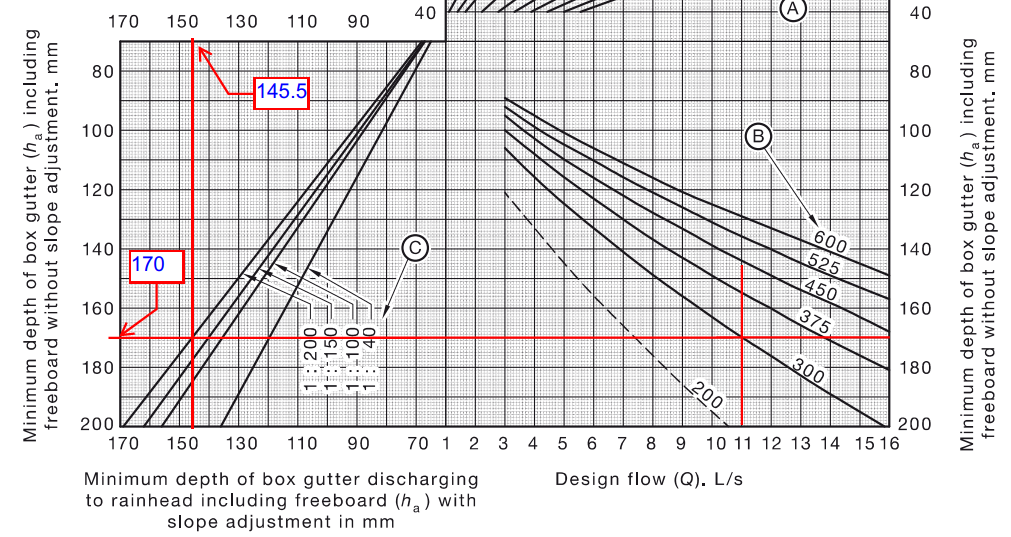
Assume our base gutter has Q1 = 5L/s, W1= 300, slope = 1:200, from Code fig I1 BGD1 = 110mm

Lets check for a new gutter with Q2=15L/s, W2 = 450, (any suitable width can be used), slope = 1:200. Multiplying factor:-

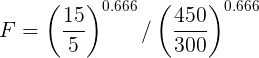
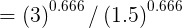
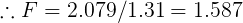
However a box gutter has a freeboard which we do not want to scale, So we take this value off the original BG depth, and add it back to the new BG depth

So new BG depth =((orig depth – freeboard) x F ) + freeboard ………..(1)

= ((110 – 58) x 1.587) + 58

= 140

= Code Depth from fig I1 (for BG Q = 15 L/s, W = 450.)

How to find the freeboard

From fig I1 look up the BG depth for both gutters, and substitute in equation 1 above.

140 = ((110 – fb) x 1.587 ) + fb. solving, fb = 58mm

This does assume the new gutter depth will be the same as the code. However checking with all other Box Gutter combinations gives the same result.

So this value works in all situations.

RWH depth, scaling factor
Similarly we can find the scaling factor for the RWH depth from the orifice formula

C_d= Coefficient of Discharge (constant)

A = Area

h = height of water over.

g = acceleration due to gravity (constant)

constants do not require scaling

Therefore are not required in the scaling factor F

…….(2)

Therefore height (ie depth of RWH) is proportional to (Q/A)²

π and 4 are constants, so can be removed

Therefore A is proportional to D²

Substitute D² for A in eqn 2

Multiplying Factor F

Example RWH depth scaling

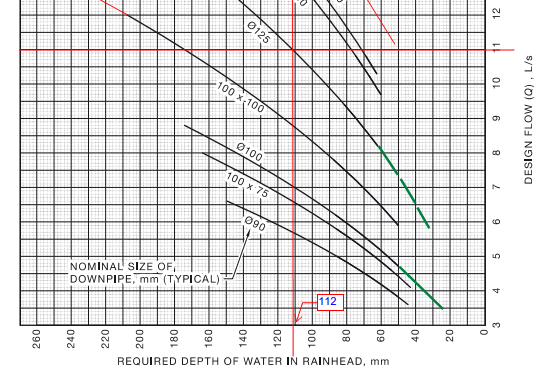
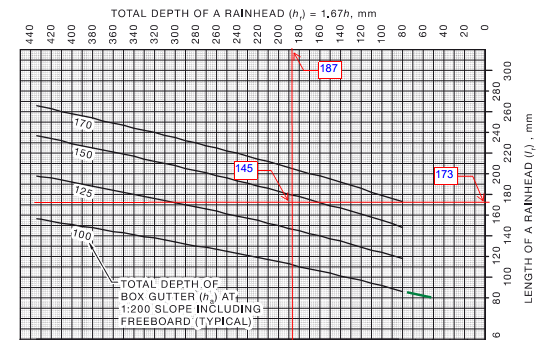
Base Gutter as before Q1 = 5L/s, W1= 300, slope = 1:200, DP1 dia = 90, from Code fig I1 BGD1 = 110mm, from fig I3 RWH1 depth = 143 RWH1 length = 119

New gutter Q2 = 15 L/s W2 = 450 DP2 = 150 (any suitable width and DP can be assumed)

However from Code note 1 fig I2 the RWH depth should be >= to DP dia x 1.25

Therefore RWH depth = 150 x 1.25 = 188 mm.

But this value does not show up on the graph. So for the purpose of the exercise we shall stick to the graph value of 167.

Because the RWH length depends on the RWH depth, Increasing the depth also increases the length, meaning that we won’t be able to check the result with the graph if we don’t use the graph calculated depth.

RWH Length, scaling factor

Similarly we can find the scaling factor for the RWH length from the trajectory formula.

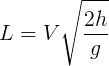
Substitute for V with V=Q/A

Substitute for A with the critical depth formula. A = W x Yc This gives:-

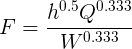
The RWH length also involves a clearance of 20.

h = RWH depth

So the new length = F x (RWH length1 – 20) + 20

Example RWH length scaling

Base Gutter as before Q1 = 5L/s, W1= 300, slope = 1:200, DP1 dia = 90, from Code fig I1 BGD1 = 110mm, from fig I3 RWH1 depth = 143 RWH1 length = 119

New gutter Q2 = 15 L/s W2 = 450 DP2 = 150 (any suitable width and DP can be assumed)

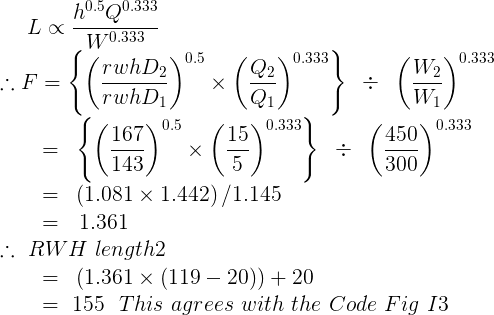
Using this method, the Box Gutter sizes for 150 L/s, width = 600, DP dia = 375, are as follows:-

Box gutter depth = 372

Box gutter width = 600

RWH depth = 433

RWH Length = 470

But is this correct?

Failing a full size test, the next best thing is Computational Fluid Dynamics. (CFD)

The simulation at the top of the page was done using these dimensions, and the flow was checked by measuring the depth at the brink.

The depth at the brink of a free outfall from a gutter = 0.7 x critical depth.

As can be seen from the simulations, there is no overflowing so the gutter works.

Compare to CSIRO formulas

K.G. Martin from the CSIRO developed formulas for roof gutter design over 40 years ago.

This is what we used before the Plumbing Code was invented.

Assuming the laws of physics haven’t changed, these formulas should still give an acceptable result

So how do they compare:-

Box gutter depth = 377 = 5mm deeper

Rain water head depth = 494 = 61mm deeper

Rain water head length = 554 = 84mm deeper.

All figures are bigger so the gutter will still work.

The box gutter depth is within an acceptable difference.

The RWH though is deeper than would be expected. Why is this?

The CSIRO formulas for the RWH depth use both the weir and the orifice formula.

The weir formula being used when the depth of water in the RWH < 1/3 DP dia.

The weir formula gives a greater depth in this situation.

The plumbing Code uses only the orifice formula. That is why we must increase the depth to 1.25 x DP dia if the calculated RWH depth < 1.25 x DPdia.

(refer to note1 figure I2) This is the cross over point of the two formulas.

so DP dia x 1.25 = 375 x 1.25 = 469 = 25mm difference. (looking incredibly reasonable)

Using this RWH depth as the new depth in the RWH length scaling factor we get:-

new RWH length = 530 = 60mm longer. (maybe a different clearance was used)

However looking at the simulation, a deeper and longer rain water head may cut down that build up on the far side.

Our gutter works, because there is a lot of tolerance built into a RWH, however to be strictly correct (with the Code) we should make these changes.

Your mission should you choose to accept it

Prove it for yourself by scaling say a 3L/s gutter up to 6, 9, and 12L/s, varying the width in each case.

All these results can be checked with the Code, figure I1 for the gutter depth, and fig I3 for the RWH sizes.

Because we are not working in fractions of a mm, and we are getting results off graphs, there could be rounding errors of a few mm’s.

Free Programs

If you don’t want to fool around with the graphs, you can get accurate interpolated results with these free programs.

However if you go above 16L/s these programs revert to formulas developed by the CSIRO, and require a small charge..

Once you have satisfied yourself that the theory works you can now:-

GO FORTH AND PROSPER

October 15, 2018

What’s the capacity of a vertical pipe?

This is a question that comes up quite often, and for a downpipe coming from an eaves gutter, it depends on the water depth over the pipe entry, and the diameter of the pipe entry.

If this water depth is less than about 1/3 of the DP dia, then the entry throat acts like a weir, and the weir formula is used, using the perimeter of the DP as the length of the weir. If the depth of water over the downpipe is greater than one-third of the down pipe diameter, then the entry throat acts more like an orifice, and the area of the downpipe is used in the orifice formulas.

This means that we either use the weir or the orifice formula.

Or if the pipe is flowing full, as in a syphonic system, we can use the pipe flowing full formulas, Colebrooke-White etc, and work out the pipe size using the hydraulic grade.

However this is not necessarily the maximum flow the downpipe can handle.

For instance, what if more water enters a downpipe from lower level roofs, balconies etc?
A plumbing stack has this situation all the time.

So now we can start to have some real fun.

When water flows down a vertical pipe (assuming it is not designed as syphonic,) the pipe does not flow full.
There is also air being pushed down, and air trying to rise up.
This is why plumbing stacks have vents all over the place, to relieve any unwanted air pressures.
Storm water pipes have entries all over the place which do the same thing.

Water starts out clinging to the sides, and as the flow gets greater it starts to spiral, and getting greater still starts to oscillate, forming plugs. Rapid oscillations develop unwanted noise and vibrations.

It has been determined (refer Standard Plumbing Engineering Design by Louis S Nielsen) that a flow which occupies about 1/4 to 1/3 of the cross sectional area of the downpipe flows without a problem.

The next thing then is to find out the terminal velocity so we can work out the flow.
We don’t need to go into that, suffice to say, that I have reduced all the formulas from the above text into something simple.
This is what can be referred to as a recommended maximum flow based on the above concepts, and equates to a flow that occupies 7/24 of the DP area.

So Q = 0.00004 * dia^2.666 where Q is in L/s, and dia in mm.

Re-arranging dia = (Q / 0.00004)^0.375

This equates to an inground pipe of the same size with a grade of about 1:100.

So, there you go, just don’t make any inground pipe smaller than the DP.

And remember, this is not the formula for designing downpipes for eaves gutters. They are designed according it to the weir, or orifice formula as stated above.

It only applies when more flow is being added to the downpipe on the way down, and the downpipe needs to be increased to handle the extra flow.

Want to impress your clients?

Turns out this is not an exact science, but just for the sake of BS..ing at design meetings, terminal velocity is about 5m/s and it takes about 2 stories to get there.

September 13, 2018

How does a CFD simulation of a Box Gutter compare to the Plumbing Code

CFD simulation of a Box Gutter

WHAT IS CFD

CFD stands for Computational Fluid Dynamics.

It is a way of generating a computer simulation of fluid flow in real time.

It consists of analyzing all forces on individual particles in the fluid. The forces can consist of gravity, viscosity, friction, surface tension, shear forces, density etc. (Nothing to do with the standard hydraulic empirical formulas.) The resultant of these forces on each particle is distributed to surrounding particles, and so on. The resulting equations must also satisfy the conservation of mass, momentum and energy.

This means millions of calculations for each frame of a video to determine how far, and in what direction, each particle will move in a given time frame. If there are 25 frames/second, a ten second video will have 250 frames, with millions of calculations for each frame.

Each fluid particle is called a cell. The smaller the cell the more accurate the simulation, (generally).

The division of the fluid into cells is called a mesh. There are millions of cells in the mesh.

The cells can be a combination of hexahedral, tetrahedral, prismatic, pyramidal or polyhedral elements.

It is a hugely time consuming process if you wish to use it in any serious way. For instance I did a CFD simulation of a much simpler thing than that shown above, and using 16 cores of computing power it took 30 hours to get a result. (and a similar amount of time to analyse the result).

However I could then read the pressure, velocity, and depth anywhere in the simulation, and all in pretty colours. But this is a huge overkill for the design of a simple box gutter.

The simulation you see above took 4 hours of computer calculation, because I used a very coarse mesh. However the result is good enough to visualize what is going on, and to prove a point.

ANALYZING THE RESULTS

The above simulation is very pretty, but not very good at measuring any meaningful depths. So lets take a closer look at the mesh.

CFD mesh simulation

The important things to note are:-

a) The deepest flow is at the upstream end, because the water surface must always fall in the direction of the flow.

b) The flow over the brink is 0.7*critical depth. This is a hydraulic principle of a free outfall from an open channel.

c) The downpipe does not flow full. The flow is restricted by the entry throat diameter.

WHAT ARE THE CODE RESULTS

The simulation is based on 11 L/s, with a 300mm wide box gutter, and no slope.

From the Plumbing Code, Fig I1 gives the gutter depth for no slope as 170, and with 1:200 slope, depth = 145 mm.

AS3500.3 Fig I1 for 11 L/s

From fig I3, for a DP dia of 125, flow = 11 L/s rainwater head details are :-

depth of water = 112

Total depth of RWH = 187,
and length of RWH, at BG depth of 145 (1:200) = 173

Fig I3 length of RWH

From Fig I6 :-

Critical depth “Loc” = 52 mm

0.7 * critical depth = 37

Fig I6 critical depth “Loc”

PLOTTING THE RESULTS ON THE MESH

Mesh Side View

The background grid is 100mm spacing, so you can visually check the dimensions, and confirm I am not pulling any legs.

The Code does not give any values for the freeboard, maybe this is because the freeboard may vary with width and flow, as in some other plumbing Codes.

However I find that a value of about 60mm seems to work. This gives a water depth of 110 mm.

The total gutter depth, and rain water head dimensions are also plotted to the code sizes.

As you can see, there is remarkable agreement with the Plumbing Code.

So we can all go away with a warm inner glow, knowing that a CFD simulation agrees with the Plumbing Code.

BTW my free programs also give the same results.

September 2, 2015

Is this strange Logic?

Cyclone Yasi

When designing box gutters to the Australian Plumbing Code AS/NZS 3500 we design them for a once in 100 year storm event.

Now, box gutters have always had a bad reputation for causing damage.

But with the advent of AS/NZS 3500 giving a concise method of designing box gutters, there should be no damage for all storms up to at least a 1 in 100 year event. (tested in the lab BTW)

Now the strange logic part. What if a hurricane or a cyclone, etc is taken as a 1 in 100 year storm event.

Our box gutter may be the least of our worries.

Cyclone Tracy

However just to protect one’s backside, in these days of litigation etc. we should make sure our box gutters are designed for a once in 100 year storm. (Besides which it is mandatory under the code)

Just in case we get a wind free cyclone.

Alternatively, I hear you ask, what about the recent floods in Dungog? Surely that was a 1 in 100 year event?

They got a lot of rain there. But not much wind.

So, when your house is floating down the river, are you going to sue your Hydraulic Consultant if your box gutter springs a leak?

On second thought, yea probably, these days.

Dungog Flood

Dungog Rainfall event

April 24, 2015

Ever wondered what angle rain falls during a once in 100 year storm?

A 1 in 100 year storm could be a typhoon, a cyclone, a hurricane, or a tornado.

These storms have very strong winds, so what happens if the rain angle is actually horizontal?

If the rain was horizontal it wouldn’t hit the ground would it?

So does the rain just keep going until it eventually evaporates?

But that can’t be right because we have floods.

And if these events are really once in 100 year storms, how come we can have one every year?

(refer to the comments below for the real answer). However continuing on for the rest of us….

The only logical answer is that the rain must come down somewhere, so once in every 100 years the rain comes down on your building.

At an angle of 63.4 degrees (2:1). Because that’s whats written in the Plumbing Code.

I reckon that rain is about 45 degrees

So it sort of takes it in turns, every 100 years your building is the lucky one, the structure at the end of the rainbow.

But not to worry, because if we use the plumbing code, we design all box gutters for this event.

We design for a 1 in 100 year storm with the rain coming down at an angle of 63.4 degrees (2:1)

April 15, 2015

HOW DOES ROOF SLOPE AFFECT THE CATCHMENT AREA?

Rainfall on a sloping roof

The Plumbing Codes have a lot of stuff on this.

But for those of us who like to delve into things, and work out how things were derived. I will attempt to offer an explanation.

The crucial thing to understand is:-

Rainfall measurements are taken in inches or millimeters falling on a horizontal surface.

The angle of the rain is not important. All that matters is the quantity of rain over a given area.

So when thinking about this, we need to calculate the area on a horizontal plane, where the rainfall would have fallen, if the roof wasn’t there. The roof intersects this amount of rainfall.

However to do this, somewhere along the line, someone has to dream up at what angle the rain is falling.

Fortunately for us, the powers that be have come up with an angle of 2:1 as shown in the diagram.

Just like anything to do with rainfall, there is no standard rainfall event.

All we can do is base the design on averages, and figures pulled out of the air.

For instance we design eaves gutters on a rainfall event that may, or may not, occur once in every 20 years.

And a rainfall angle of 2:1 is as good as any, and in fact, as you will see later, this makes the calculations much easier.

Looking at the diagram, a roof from A to D also intersects the same amount of rain as the main roof.
In fact any roof between rainfall lines B and C, will intersect the same amount of rain, and therefore have the same catchment area.

But what is really interesting, it doesn’t matter what the roof does to get from point A to point D.

It can go up and down. or round and round.

As long as the starting point is A, and the ending point is D, it will have the same catchment area.

Roof with vertical drop

Now, to determine what the real catchment area is, we must determine the area of the slope effect that must be added.

For a straight roof the Architect has normally shown this slope on the drawings. But if there are vertical drops, or different slopes we take the average as shown in the diagram. because this will intersect the same amount of rain.

Now the hard part, we have to do some mathematics.

We know the rain falls at an angle of 2:1, therefore in the diagram above, the length of the “slope effect added”, is half the “vertical rise” ( 2:1 remember).

This is also true for the roof areas, that is, the area of the slope effect is half the area of the vertical rise, as both these lengths are multiplied by the same roof width to find the area.

So all we have to do now is find the area of the vertical rise.

If you can remember your trigonometry, the vertical rise area = (roof plan area) * tan( roof slope).

Catchment area (CA) = roof plan area + 1/2 (vertical rise area)

= roof plan area + 1/2 *( roof plan area * tan (roof slope)

Ah, on second thoughts, its probably just as easy to look up the “slope factor” in the Plumbing Code, or simply measure the area from the Architects Elevations.

Any questions?

April 14, 2015

What is a Rain Shadow? and why do I need to know?

When designing roof gutters, or surface drainage for building sites, The rain shadow can make a big difference. Especially for a tall building.

The Plumbing Codes assume rain is coming down at an angle of 2:1.

That is 2 units vertical to 1 unit horizontal. (63.4 degrees).

So from the diagram on the left, you can see the effect of the shadow.

The area of the shadow is half the area of the vertical face of the building. (2:1remember).

But what if rain comes from the other direction?

From the diagram on the right, you can see that half the vertical face of the building has been added to the catchment area.

The catchment area is always measured on the horizontal plane. Because that’s how they measure rainfall when they talk about ‘mm’ or ‘inches’ of rain. So to make all our hydraulic formulas work, we must also use this method if we want to use rainfall figures calculated by the local Weather Bureau.

Now consider the interesting case where we have a building on both sides. One side has the shadow, and the other has the added catchment. If the buildings were of equal height, the effects would cancel each other out. No matter which direction the rain came from. Even if the rain came down the middle.

Got your head around that one yet?

However if the rain came from all directions at once, we are in diabolical trouble, and our roof gutter design, or site storm water design would be the least of our worries.