The Plumbing Codes have a lot of stuff on this.

 

But for those of us who like to delve into things, and work out how things were derived. I will attempt to offer an explanation.

 

The crucial thing to understand is:-

 

  Rainfall measurements are taken in inches or millimeters falling on a horizontal surface.

 

The angle of the rain is not important. All that matters is the quantity of rain over a given area.

 

So when thinking about this, we need to calculate the area on a horizontal plane, where the rainfall would have fallen, if the roof wasn’t there. The roof intersects this amount of rainfall.

 

However to do this, somewhere along the line, someone has to dream up at what angle the rain is falling.

 

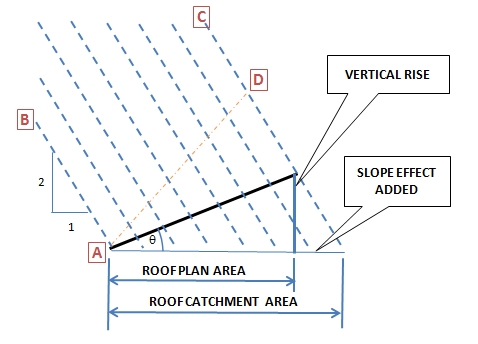
Fortunately for us, the powers that be have come up with an angle of 2:1 as shown in the diagram.

 

Just like anything to do with rainfall, there is no standard rainfall event.

All we can do is base the design on averages, and figures pulled out of the air.

 

For instance we design eaves gutters on a rainfall event that may, or may not, occur once in every 20 years.

And a rainfall angle of 2:1 is as good as any, and in fact, as you will see later, this makes the calculations much easier.

 

Looking at the diagram, a roof from A to D also intersects the same amount of rain as the main roof.
In fact any roof between rainfall lines B and C, will intersect the same amount of rain, and therefore have the same catchment area.

 

But what is really interesting,  it doesn’t matter what the roof does to get from point A to point D.

It can go up and down. or round and round.

As long as the starting point is A, and the ending point is D, it will have the same catchment area.

 

Now, to determine what the real catchment area is, we must determine the area of the slope effect that must be added.

 

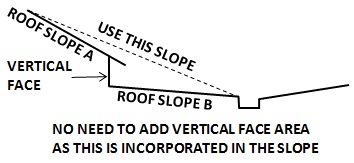
For a straight roof the Architect has normally shown this slope on the drawings. But if there are vertical drops, or different slopes we take the average as shown in the diagram. because this will intersect the same amount of rain.

 

Now the hard part, we have to do some mathematics.

We know the rain falls at an angle of 2:1, therefore in the diagram above, the length of the “slope effect added”, is half the “vertical rise” ( 2:1 remember).

 

This is also true for the roof areas, that is, the area of the slope effect is half the area of the vertical rise, as both these lengths are multiplied by the same roof width to find the area.

 

So all we have to do now is find the area of the vertical rise.

If you can remember your trigonometry, the vertical rise area = (roof plan area) * tan( roof slope).

 

Catchment area (CA)  = roof plan area + 1/2 (vertical rise area)

= roof plan area  +  1/2 *( roof plan area * tan (roof slope)

 

Ah, on second thoughts, its probably just as easy to look up the “slope factor” in the Plumbing Code, or simply measure the area from the Architects Elevations.

Any questions?